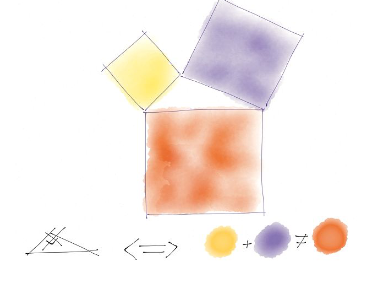
Math & construction !

Nous voici bâtisseurs, au temps des grandes pyramides d’Égypte, un fil ou une corde à la main. La pyramide que nous allons édifier sera construite sur une basse carrée la plus parfaite possible.

Il
est
facile
de tracer
un losange
à l’aide
d’un
fil.

Mais comment réaliser un angle droit afin d’obtenir un carré ?

Nous avons découvert
la corde à 13 nœuds et son triangle.
Notre idée a été validée par Géogebra.

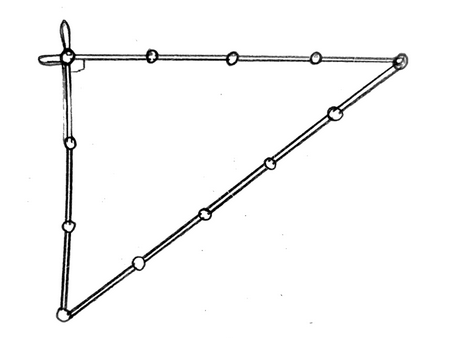
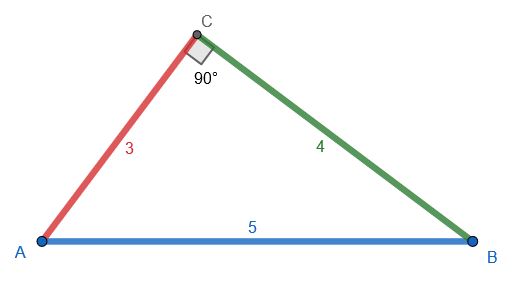
Ce triangle forme le triplet 3-4-5.

Parmi tous les triangles, comment reconnaître parfaitement ceux qui sont rectangles et ceux qui ne le sont pas ?

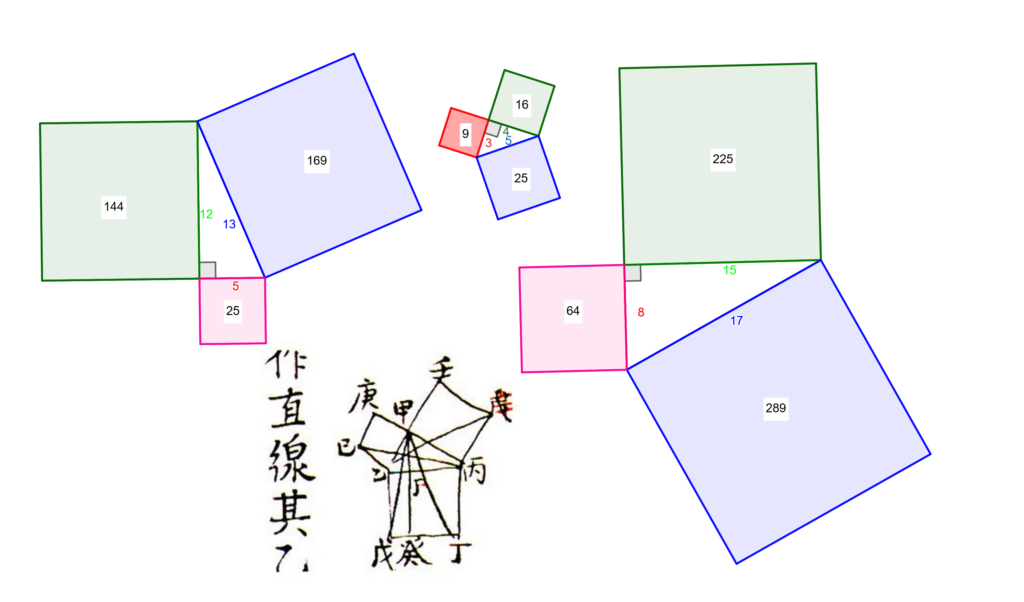
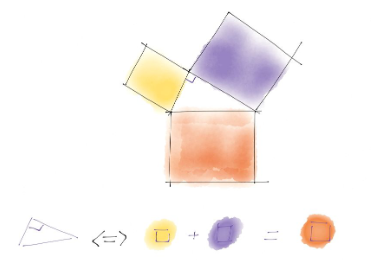
Nous observons que :
l’aire du grand carré est égale à la somme
des aires des deux autres carrés.

Nous conjecturons que
notre observation fonctionne
pour tous les triangles rectangles.

Nous venons de découvrir
le Théorème de Pythagore
présenté dans ce conte mathématique.

Une simple corde nous a permis de découvrir l’un des résultats les plus célèbres et les plus fondamentaux des Mathématiques.

et